中1数学「正負の数（加法・減法）」計算問題のミスを減らす方法

前回は、中1数学「正負の数（知識問題）」の解説を扱いました。

今回はその第二弾として、正負の数（加法減法）の解説になります。

いかにして、計算ミスを減らすかにポイントを絞っています。

：自己紹介はコチラ

基本的な内容ですが、数学が苦手な生徒の多くは順序や決まりの理解が不十分です。

また、伸び悩む生徒は、無駄が多い、計算ミスしやすい解き方の癖が付いています。

抜け漏れや勘違いをして覚えている所がないか、点検するつもりで解いて下さい。
（内容自体は簡単です）

計算能力を高めていく上で、私が重要視していた点です。

数学の成績を上げていくためには、どれも重要な項目です。

意識しながら次の問題に取り組み、解説に進んでください。

例題

・３題あるので実際に、ノート等で解いてみてください。

・★は難易度を表しているので、目安にしてください。

練習問題（１）★☆☆☆☆

\(次の式のカッコを外しなさい。\) \(~~~~~~(-5)+(-5)-(-5)-(+5)+(+5)\)

（１）解説

練習問題（２）★☆☆☆☆

\(次の計算をしなさい。\) \(~~~~~~(-39)+(-45)-(-51)-(+75)+(+95)\)

解説（２）

練習問題（３）★★☆☆☆

\(次の計算をしなさい。\) \(~~~~~~(-\frac{3}{8})+(-\frac{5}{6})-(-\frac{7}{3})\) \(-(+1.25)\)

解説（３）

解説

今回の単元（計算）で重要なのは、合っているか否かよりも「手順」です。数学試験における失点の大半はミスによるものです。

ミスをするのには、それなりの原因があります。答えにたどりつくまでに、ミスをする可能性はできるだけ除く工夫が必要です。

手順や式の書き方が、だいたい一致していれば大丈夫ですので、自分の途中式と見比べてみて、取り入れられそうな部分は取り入れてください。

（１）の解説と攻略のポイント

確認すべきところは、簡単です。

カッコの内と外を見てください。

\(~~~~~~(-5)+(-5)-(-5)-(+5)+(+5)\)

〇…カッコ内の符号のみ
　→カッコ内の符号のまま

〇…カッコ内外が異なる符号
　→－（マイナス）になる

〇…カッコ内と外が同じ符号
　→＋（プラス）になる

非常にシンプルなルールですので、サクッと覚えて癖にしましょう。

ちなみに、念のため、
ここでこの問題を扱った理由はコチラです。

（興味がない人は飛ばしてください）

\(~~~~~~(-8)-(-5)=(-8)+(+5)\) \(~~~~~~~~~~~~~~~~~~~~~~~~~~~=-(8-5)\) \(~~~~~~~~~~~~~~~~~~~~~~~~~~~=-3\)

学校では一番最初、このような習い方をします。詳しい手順説明は省きますが、実際に問題を解くときは、「減法は加法に直して…」なんてこと誰もやりません…。

と思われるかもしれませんが、私も同感です。理由はさておき、混乱の原因になるケースも多く見てきましたので、「これはこれ」として分けて理解できれば十分です。

詳しい説明はコチラをどうぞ
：正負の数の加法と減法（中学校数学学習サイト）

（２）の解説と攻略のポイント

カッコの外し方については触れたので、次は計算手順です。

\(次の計算をしなさい。\) \(~~~~~~(-39)+(-45)-(-51)-(+75)+(+95)\) \(~~~~=\) \(-39-45\) \(+51\) \(-75\) \(+95\) \(~~~~=\) \(-159\) \(+146\) \(~~~~=\) \(-13\)

カッコを外した後は

・負の数と正の数をそれぞれまとめる
 （チームごとに集合するイメージ）

・絶対値の大きい符号を書き差を求める
 （正と負で勝負をするイメージ）

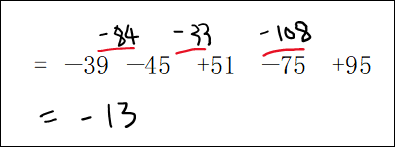
途中式をみると、このように左から順に計算していくパターンをよく見かけますが、あまりお勧めしません。計算回数は同じですが、足したり引いたり1回1回判断しなければならず、途中式も分かりにくいので、もし癖がついていたら、直した方が良いでしょう。

（３）の解説と攻略のポイント

分数と小数が混ざった加法、減法の計算です。

基本的には、
・カッコを外す→チーム分け→勝負

この流れに従って進めていきます。

まずはカッコを外し、小数を分数に揃えるところまで。

\(次の計算をしなさい。\) \(~~~~~~(-\frac{3}{8})+(-\frac{5}{6})-(-\frac{7}{3})\) \(-(+1.25)\) \(~~~~=-\frac{3}{8}-\frac{5}{6}+\frac{7}{3}\) \(-\frac{5}{4}\)

ここからチーム分けですが、その前にこのように通分しましょう。

\(~~~~~~(-\frac{3}{8})+(-\frac{5}{6})-(-\frac{7}{3})\) \(-(+1.25)\) \(~~~~=-\frac{3}{8}-\frac{5}{6}+\frac{7}{3}-\frac{5}{4}\) \(~~~~=\) \(\frac{~~-9~~-20~~+56~~-30~~}{24}\)

分母の（８・６・３・４）の最小公倍数２４で通分し、分子はこのように1本線の上にすべて並べてしまいます。あとは分子の計算をするのみです。

\(~~~~~~(-\frac{3}{8})+(-\frac{5}{6})-(-\frac{7}{3})\) \(-(+1.25)\) \(~~~~=-\frac{3}{8}-\frac{5}{6}+\frac{7}{3}-\frac{5}{4}\) \(~~~~=\frac{~~-9~~-20~~+56~~-30~~}{24}\) \(~~~~=\frac{~~-~~59~~~~+~~56~~}{24}\) \(~~~~=-\frac{1}{8}\)

特に習い始めは、見慣れない分数の形ですが、後々増えてくるので早々に慣れた方がよいです。また、計算ミスを減らすことにもつながります。

・マイナスを書く位置（真ん中）
・約分

初歩的な内容ですが、失点の原因になるので最後まで確認しましょう。

解説のまとめ

今回は計算中心の内容でした。計算はとにかく手順理解といかにシンプルに解くかが正答率UPのポイントです。

正しい型を身に付けるためには、意識しなくてもできるよう、たくさん練習を積むことが重要です。ここは頑張りましょう。

練習問題と参考書

<中学校数学学習サイト>

・正負の数（加法）

・正負の数（減法）

・正負の数（加法と減法）

問題量が豊富で印刷可能、すぐに解答を確認できるのでお勧めです。
終わった人は、総合問題（基本・標準）にチャレンジしましょう。

・中学校数学学習サイト（総合問題・基礎問題）

---

<参考書>

こちらは、塾講師時代にテスト対策序盤で頻繁に使用していた教材です。

他に気に入っているのがあれば、それでも構いません。

・中学教科書ワーク 東京書籍版 新編 新しい数学 1年 (日本語) 単行本 –

購入時、未成年の方は保護者の方に必ず確認してましょう。
「〇〇版」の部分を自分の教科書に合わせて変更することをお忘れなく。

（一覧を掲載した記事もあります。記事最下段。）